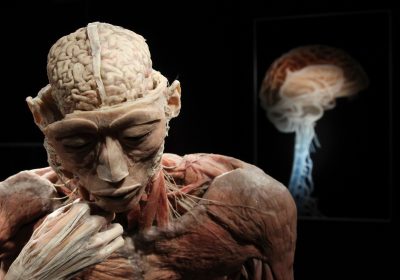
編織可能是人類最古老的技藝之一，也是物理學家 Elisabetta Matsumoto 的靈感來源，透過分析編織的數學原理，可訓練電腦如編織一樣思考，編寫新的運算程序。
她的研究基於紐結理論（Knot Theory），以數學原理來解釋紐結方式，有助解釋 DNA 展合、分子組成，以及分子的空間分佈，如何賦予其物理和化學特性。
紐結理論是拓撲學（Topology）的一個分支，就其中的物理紐結而言，可以通過研究扭曲或壓縮之變形來計算織物的彈性。19 世紀初期，紐結理論的重點是研究所謂的「原子紐結」（原子的渦旋模式），當時的物理學家和數學家所得到的紐結參考甚為有限，研究的通常是船索等商用或農用繩結，普遍大而笨重；相比之下，編織或鉤編的結在拓撲幾何學上更形複雜，編織或鉤編的結，採用針腳之間相連的方式，而不至於散開。
Matsumoto 解釋：「編織時，針腳的不同類型、幾何形狀之間的差異，以及在織物中的排序，對織物的性能有決定作用。」只要輕微更改打結的方式，譬如更改針腳的交叉點，便能影響整體織物的力學。只以下針或上針編織，通常都造成織物邊角捲起；將下針和上針交替編織，便能解決這個問題。
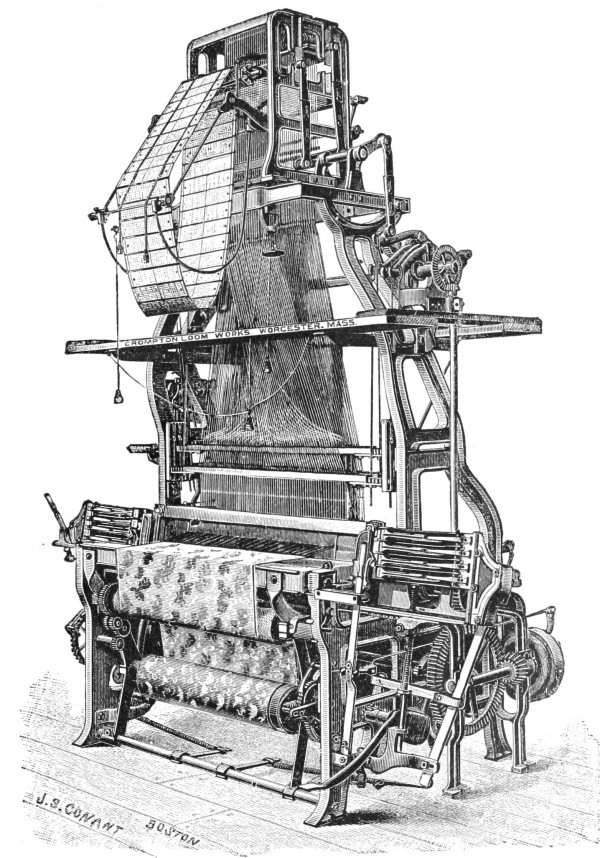
正是由於編織本身有其「內在程序」，1804 年面世的雅卡爾織布機（Jacquard machine），便被視為歷史上最早的計算機。它使用機械打孔卡來指示織機的交叉方向，控制經線與緯線的關係，得出不同織紋。現代電腦的計算法，是將二進制的 0 和 1，轉換為圖形和計算結果，對織布機而言，針腳的不同順序，也能編寫織物的機械性能，上針和下針，便是編織語言的 0 和 1。
在 Matsumoto 看來，編織帶著一套非常複雜的文法系統，可以將其轉換為計算程序：「透過為編織系統建立字母或單詞順序，最終得出的織物，也將具有不同的機械性能。」她的研究項目得到美國國家科學基金會贊助，目標是將物理性質的剛度和彈性，轉換為公式，利用織物的彈性和可變形等特性來解釋。
如果能找到這條公式，不僅對純數和理論紐結的研究有重大意義，也將帶來應用數學的變革，可運用於訂製假肢，可穿戴醫療設備，或者製造超級柔韌的新材料：譬如節省服裝製造的成本，減輕由速食時尚造成的經濟負擔；若有朝一日太空人飛往火星，他們亦會需要足夠阻擋太空輻射的太空服。
